Question

Given P(A and B) 0.20, P(A) 0.49, and P(B) = 0.41 are events A and B independent or dependent? 1) Dependent 2) Independent

Answer 1

Answer: The correct option is (1) Dependent.

Step-by-step explanation: For two events, we are given the following values of the probabilities :

P(A ∩ B) = 0.20, P(A) = 0.49 and P(B) = 0.41.

We are to check whether the events A and B are independent or dependent.

We know that

the two events C and D are said to be independent if the probabilities of their intersection is equal to the product of their probabilities.

That is, P(C ∩ D) = P(C) × P(D).

For the given two events A and B, we have

`P(A)* P(B)=0.49*0.41=0.2009\\eq P(A\cap B)=0.20\\\\\Rightarrow P(A\cap B)\\eq P(A)* P(B).`

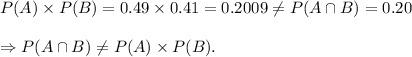
Therefore, the probabilities of the intersection of two events A and B is NOT equal to the product of the probabilities of the two events.

Thus, the events A and B are NOT independent. They are dependent events.

Option (1) is CORRECT.