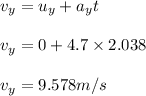Question

A particle starts from the origin at t = 0 with an initial velocity of 5.3 m/s along the positive x axis.If the acceleration is (-2.6 i^ + 4.7 j^)m/s2, determine (a)the velocity and (b)position of the particle at the moment it reaches its maximum x coordinate.

Answer 1

Velocity at the point of maximum x cordinate is 9.578m/s

Position vector of the particle when it reaches point of maximum x ordinate is
`\overrightarrow{r}=5.402\widehat{i}+9.76\widehat{j}`

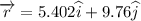
Step-by-step explanation:

We shall resolve the motion of the particle along x and y direction separately

The particle will reach it's maximum x coordinate when it's velocity along x axis shall become 0

We have acceleration along x-axis =
`-2.6m/s^(2)`

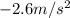
acceleration along y-axis =
`4.7m/s^(2)`

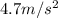
Thus using the first equation of motion along x axis we get

`v_(x)=u_(x)+a_(x)t\\\\`

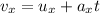
Applying values we get

`0=5.3-2.6t\\\\\therefore t=(5.3)/(2.6)sec\\\\t=2.038sec`

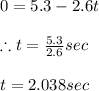
Now to obtain it's position we shall use third equation of motion

`v_(x)^(2)=u_(x)^(2)+2as_(x)\\\\0=(5.3)^(2)+2(-2.6)s_(x)\\\\\therefore s_(x)=(-28.09)/(-5.2)m\\\\s_(x)=5.402m`

Now it's location along y- axis can be obtained using 2nd equation of motion along the y axis

`s_(y)=u_(y)t+(1)/(2)a_(y)t^(2)`

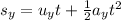
Applying values as follows we get

`u_(y)=0\\a_(y)=4.7m/s^(2)\\t=2.038s`

`s_(y)=0* 2.038+(1)/(2)* 4.7m/s^(2)*2.038^(2)\\\\s_(y)=9.76m`

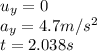
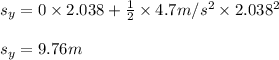
thus the position vector of the particle when it reaches it's maximum x co-ordinate is

`\overrightarrow{r}=5.402\widehat{i}+9.76\widehat{j}`

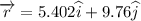
Now velocity of the particle at the position of maximum x co-ordinate shall be zero along x-axis and along the y-axis it can be found along the first equation of motion along y axis

`v_(y)=u_(y)+a_(y)t\\\\v_(y)=0+4.7* 2.038\\\\v_(y)=9.578m/s`