Answer:
The solution of the given initial value problems in explicit form is
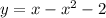 and the solutions are defined for all real numbers.
and the solutions are defined for all real numbers.
Explanation:
The given differential equation is
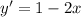
It can be written as

Use variable separable method to solve this differential equation.

Integrate both the sides.
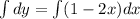
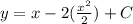
![[\because \int x^n=(x^(n+1))/(n+1)]](https://img.qammunity.org/2020/formulas/mathematics/college/d9uw45lhogrstavfc0mug0gbzjpwxw9x73.png)
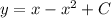 ... (1)
... (1)
It is given that y(1) = -2. Substitute x=1 and y=-2 to find the value of C.
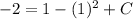

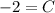
The value of C is -2. Substitute C=-2 in equation (1).
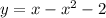
Therefore the solution of the given initial value problems in explicit form is
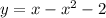 .
.
The solution is quadratic function, so it is defined for all real values.
Therefore the solutions are defined for all real numbers.