Answer:
Explanation:
Given lines in parametric form
line
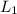
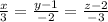
direction vector of

Line

direction vector of
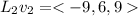
therefore

thus lines are parallel.
(ii)distance between two lines is
 is given by
is given by
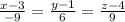 =s
=s
 =3s
=3s
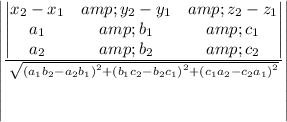
where
 =3
=3
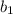 =-2
=-2
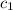 =-3
=-3
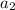 =-9
=-9
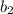 =6
=6
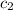 =9
=9
distance(d)=0 units since value of the matrix
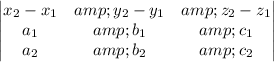
is zero