Question

Maloney, Inc., has an odd dividend policy. The company has just paid a dividend of $7 per share and has announced that it will increase the dividend by $6 per share for each of the next five years, and then never pay another dividend. If you require a return of 14 percent on the company’s stock, how much will you pay for a share today?

Answer 1

i will pay $80.47 or lower, to achieve 14% yield or higher.

Step-by-step explanation:

We have to calcualte the present value of the dividends cash flow.

because the dividends will growth until a certain date, we cannot use the gordon model.

`\left[\begin{array}{ccc}Month&Dividend&PV&Year1&13&11.40&Year2&19&14.62&Year3&25&16.874&Year4&31&18.35&Year5&37&19.21&Year6&43&19.591&Intrinsic&Value&80.47\end{array}\right]`

For each dividend, we do previous year + 6

Then for Present value:

`(Dividends)/((1 + rate)^(time) ) = PV`

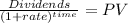
for example year 3

`(25)/((1.14)^(3) ) = 16.874`