Answer:
The probability of her picking both out in a sequence would be

Explanation:
Hello, this is a great question and one that many people struggle with in school. Hopefully I can help you understand it more clearly. Kelly has 11 markers in total within her backpack and needs to randomly pick out the pink marker. since there is only 1 that would mean her probability of picking out the pink marker is 1/11 .
Now there are 10 markers inside the backpack and she needs to randomly pick out the blue marker. since there is only 1 blue marker that would mean her probability of picking that one out is 1/10.
So now we have the following probabilities
- 1/11 for the pink marker
- 1/10 for the blue marker
Now if we want to find the probability of her getting the pink marker and the blue marker one after another we would need to multiply both fractions together
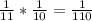
So the probability of her picking both out in a sequence would be
