Question

Factor f(x) = 15x^3 - 15x^2 - 90x completely and determine the exact value(s) of the zero(s) and enter them as a comma separated list. x =

Answer 1

`x=-2,0,3`

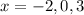
Explanation:

We have been given a function
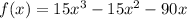`f(x)=15x^3-15x^2-90x`. We are asked to find the zeros of our given function.

To find the zeros of our given function, we will equate our given function by 0 as shown below:

`15x^3-15x^2-90x=0`

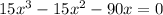
Now, we will factor our equation. We can see that all terms of our equation a common factor that is
`15x`.

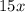Upon factoring out
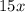`15x`, we will get:

`15x(x^2-x-6)=0`

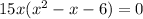
Now, we will split the middle term of our equation into parts, whose sum is
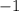`-1` and whose product is
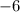`-6`. We know such two numbers are
`-3\text{ and }2`.

`15x(x^2-3x+2x-6)=0`

`15x((x^2-3x)+(2x-6))=0`

`15x(x(x-3)+2(x-3))=0`

`15x(x-3)(x+2)=0`

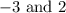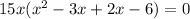
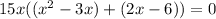
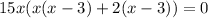
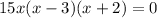
Now, we will use zero product property to find the zeros of our given function.

`15x=0\text{ (or) }(x-3)=0\text{ (or) }(x+2)=0`

`15x=0\text{ (or) }x-3=0\text{ (or) }x+2=0`

`(15x)/(15)=(0)/(15)\text{ (or) }x-3=0\text{ (or) }x+2=0`

`x=0\text{ (or) }x=3\text{ (or) }x=-2`

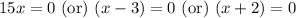
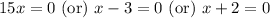
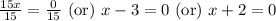
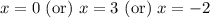
Therefore, the zeros of our given function are
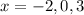`x=-2,0,3`.