Question

Determine whether lines L1 and L2 passing through the pairs of points are parallel, perpendicular, or neither. L1 : (–5, –5), (4, 6) L2 : (–9, 8), (–18, –3)

Answer 1

Parallel

Explanation:

Answer 2

Answer: The lines L1 and L2 are parallel.

Step-by-step explanation: We are given to determine whether the following lines L1 and L2 passing through the pair of points are parallel, perpendicular or neither :

L1 : (–5, –5), (4, 6),

L2 : (–9, 8), (–18, –3).

We know that a pair of lines are

(i) PARALLEL if the slopes of both the lines are equal.

(II) PERPENDICULAR if the product of the slopes of the lines is -1.

The SLOPE of a straight line passing through the points (a, b) and (c, d) is given by

`m=(d-b)/(c-a).`

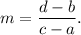
So, the slope of line L1 is

`m_1=(6-(-5))/(4-(-5))=(6+5)/(4+5)=(11)/(9)`

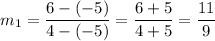
and

the slope of line L2 is

`m_2=(-3-8)/(-18-(-9))=(-11)/(-9)=(11)/(9).`

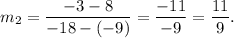
Therefore, we get

`m_1=m_2\\\\\Rightarrow \textup{Slope of line L1}=\textup{Slope of line L2}.`

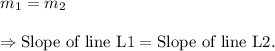
Hence, the lines L1 and L2 are parallel.