Answer:
Yes! There are 3 different explanations I have. Pick your favorite.
Explanation:
So we are asked to see if the following equation holds:
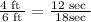
The units cancel out ft/ft=1 and sec/sec=1.
So we are really just trying to see if 4/6 is equal to 12/18
Or you could cross multiply and see if the products are the same on both sides:

Cross multiply:
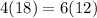
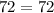
Since you have the same thing on both sides then the ratios given were proportional.
OR!
Put 4/6 and 12/18 in your calculator. They both come out to have the same decimal expansion of .66666666666666666(repeating) so the ratios gives are proportional.
OR!
Reduce 12/18 and reduce 4/6 and see if the reduced fractions are same.
12/18=2/3 (I divided top and bottom by 6)
4/6=2/3 (I divided top and bottom by 2)
They are equal to the same reduced fraction so they are proportional.