Question

Construct a polynomial function with the following properties: fifth degree, 2 is a zero of multiplicity 3, -2 is the only other zero, leading coefficient is 2.

f(x)=?​

Can some help?

Answer 1

`f(x)=2(x-2)^(3)(x+2)^(2)`

Explanation:

we know that

2 is a zero of multiplicity 3 of the polynomial

so

we have that

x=2 is a solution of the polynomial

A factor of the polynomial is

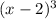`(x-2)^(3)` ----> is elevated to the cube because is a multiplicity 3

and the other solution is x=-2

since the polynomial is fifth degree, x=-2 must have a multiplicity 2

so

the other factor of the polynomial is

`(x+2)^(2)` ----> is squared because is a multiplicity 2

therefore

The polynomial is equal to multiply the factors by the leading coefficient

so

`f(x)=2(x-2)^(3)(x+2)^(2)`