Question

Critical Thinking and Statistics The average test score of the class was an 80 and the standard deviation was 2. About 68 % of the class would score between what 2 values? 80 and 82 78 and 82 76 and 84 74 and 86

Answer 1

B. 78 and 82.

Explanation:

We have been given that the average test score of the class was an 80 and the standard deviation was 2. We are asked to find two values between which 68% of class will score.

We know that in a normal distribution approximately 68% of the data falls within one standard deviation of the mean.

So 68% scores will lie within one standard deviation below and above mean that is:

`(\mu-\sigma,\mu+\sigma)`

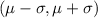
Upon substituting our given values, we will get:

`(80-2,80+2)`

`(78,82)`

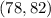
Therefore, about 68% of the class would score between 78 and 81 and option B is the correct choice.