Question

Factor completely 3x² − x − 4.
20 for the top answer

Answer 1

`(3x-4)(x+1)`

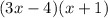
Explanation:

This is in the form
`ax^2+bx+c`.

If your wish is to factor by grouping, then you goal is too look for two numbers that multiply to be
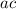`ac` and adds up to be
`b`.

Then once you find those numbers you replace b with those numbers. Then the factor by grouping can be done.

So you have
`a=3,b=-1,c=-4`

`ac=3(-4)`

`b=-1`

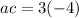
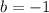
The numbers that we need are already present since -4+3 is -1.

So replace -1 in

`3x^2-1x-4`

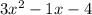
with (-4+3)

`3x^2-4x+3x-4`

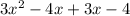
Now group the first two terms together and group the last two terms together:

`(3x^2-4x)+(3x-4)`

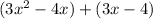
Factor what you can from both pairs:

`x(3x-4)+1(3x-4)`

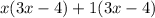
Notice you have two terms: x(3x-4) and 1(3x-4). These terms have a common factor of (3x-4) so factor that out of our expression like so:

`(3x-4)(x+1)`

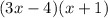
Check with foil if you like:

First: 3x(x)=3x^2

Outer: 3x(1)=3x

Inner: -4(x)=-4x

Last: -4(1)=-4

----------------------Add together:

3x^2-x-4

Answer 2

Answer:
`=(3x-4)(x+1)`

Explanation:

Given the polynomial
`3x^2- x -4`

We can observe that it is written in this form:

`ax^2+bx+c`

To factor completely, we need to follow these steps:

- Rewrite the term "b" as the sum of two terms whose product be
`(3)(-4)=-12` and whose sum be -1:

`=3x^2+(-4+3)x-4`

- Applying Distributive property, we get:

`=3x^2-4x+3x-4`

- Make two groups of two terms each:

`=(3x^2-4x)+(3x-4)`

- Factor out "x" from the first group and 1 from the second group:

`=x(3x-4)+1(3x-4)`

- Factoring out
`(3x-4)`, we get:

`=(3x-4)(x+1)`