Question

As you stand by the side of the road, a car approaches you at a constant speed, sounding its horn, and you hear a frequency of 76 Hz. After the car goes by, you hear a frequency of 65 Hz. What is the speed of the car? The speed of sound in the air is 343 m/s.

Answer 1

26.8 m/s

Step-by-step explanation:

`v` = constant speed of the car

`V` = speed of sound = 343 m/s

`f` = actual frequency of the horn

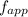`f_(app)` = frequency heard as the car approach = 76 Hz

frequency heard as the car approach is given as

`f_(app)=(vf)/(V - v)`

`76 =(vf)/(343 - v)` eq-1

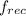`f_(rec)` = frequency heard as the car recedes = 65 Hz

frequency heard as the car goes away is given as

`f_(rec)=(vf)/(V + v)`

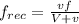
`65 =(vf)/(343 + v)` eq-2

dividing eq-1 by eq-2

`(76)/(65)=(343+v)/(343-v)`

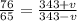
`v` = 26.8 m/s