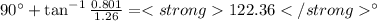Question

Charge 1 of +4 micro-coulombs is placed at the origin, charge 2 of +18 micro-coulombs is placed at x = +0.32 m, y = -0.59 m, charge 3 of -2 micro-coulombs is placed at x = -0.79 m, y = 0 m. Measured counter-clockwise in degrees, what is the angle of the total electric force vector on charge 1?

CORRECT ANSWER: 122.36

Answer 1

122.36

Step-by-step explanation:

The distance (d) between Charge 1 and 2 can be calculated as:

`d=√(0.32^2+0.59^2)=0.67m`

The force between them is given as

`F_1=(1)/(4\pi \epsilon_0)(4*18*10^-12)/(0.67^2)= 1.44N`

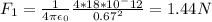
The angle of this force with positive x-axis is given as

`\theta_1=90^(\circ)+\tan^(-1)(0.32)/(0.59)=118.47^(\circ)`

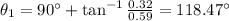
Now,

The force between 1 and 3 is

`F_2=(1)/(4\pi \epsilon_0)(4*2*10^(-12))/(0.79^2)= 0.115N`

As the force is attractive it is along negative x direction so the angle will be given as =
`\theta_2 = 180^(\circ)`

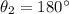
So the negative x component of the resultant force will be calculated as

=
`1.44\cos(180-118.47)^(\circ)+0.115=0.801`

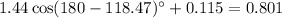
And the positive y component =
`1.44\sin(180-118.47)^(\circ)=1.26`

So the angle of the resultant with positive x axis will be

`90^(\circ)+\tan^(-1)(0.801)/(1.26)=<strong>122.36</strong>^(\circ)`