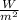Question

Atmospheric air at 25 °C and 8 m/s flows over both surfaces of an isothermal (179C) flat plate that is 2.75m long. Determine the heat transfer rate per unit from the plate for 3 width different values of the critical Reynolds number: 100,000; 500,000; and 1,000,000

Answer 1

Re=100,000⇒Q=275.25
`(W)/(m^2)`

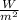
Re=500,000⇒Q=1,757.77
`(W)/(m^2)`

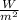
Re=1,000,000⇒Q=3060.36
`(W)/(m^2)`

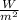
Step-by-step explanation:

Given:

For air
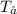`T_∞`=25°C ,V=8 m/s

For surface
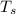`T_s`=179°C

L=2.75 m ,b=3 m

We know that for flat plate

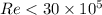`Re<30*10^5`⇒Laminar flow

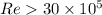`Re>30*10^5`⇒Turbulent flow

Take Re=100,000:

So this is case of laminar flow

`Nu=0.664Re^{(1)/(2)}Pr^{(1)/(3)}`

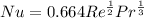
From standard air property table at 25°C

Pr= is 0.71 ,K=26.24
`* 10^(-3)`

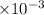
So
`Nu=0.664* 100,000^{(1)/(2)}* 0.71^{(1)/(3)}`

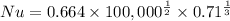
Nu=187.32 (
`(hL)/(K_(air))`)

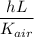187.32=
`(h*2.75)/(26.24* 10^(-3))`

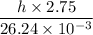
⇒h=1.78
`(W)/(m^2-K)`

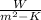
heat transfer rate =h
`(T_∞-T_s)`

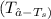
=275.25
`(W)/(m^2)`

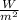
Take Re=500,000:

So this is case of turbulent flow

`Nu=0.037Re^{(4)/(5)}Pr^{(1)/(3)}`

`Nu=0.037* 500,000^{(4)/(5)}* 0.71^{(1)/(3)}`

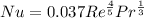
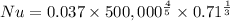
Nu=1196.18 ⇒h=11.14
`(W)/(m^2-K)`

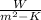
heat transfer rate =h
`(T_∞-T_s)`

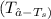
=11.14(179-25)

= 1,757.77
`(W)/(m^2)`

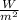
Take Re=1,000,000:

So this is case of turbulent flow

`Nu=0.037Re^{(4)/(5)}Pr^{(1)/(3)}`

`Nu=0.037* 1,000,000^{(4)/(5)}* 0.71^{(1)/(3)}`

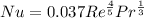
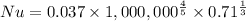
Nu=2082.6 ⇒h=19.87
`(W)/(m^2-K)`

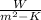
heat transfer rate =h
`(T_∞-T_s)`

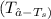
=19.87(179-25)

= 3060.36
`(W)/(m^2)`