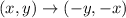Question

Which of the following is the rule for rotating the point with coordinates (x,y), 180° counterclockwise about the origin?

A. (x,y) → (y,x)
B. (x,y) → (y,-x)
C. (x,y) → (-y,-x)
D. (x,y) → (-x,-y)
​

Answer 1

The correct option is D.

Explanation:

If a point rotating 180° counterclockwise about the origin, then the sign of each coordinate is changed.

Consider the coordinates of a point are (x,y).

If a (x,y) rotating 180° counterclockwise about the origin, then the rule of rotation is defined as

`(x,y)\rightarrow (-x,-y)`

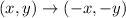
In which (x,y) is the coordinate pair of preimage and (-x,-y) is the coordinate pair of image.

Therefore the correct option is D.

If a point reflects across the line y=x , then

`(x,y)\rightarrow (y,x)`

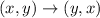
If a point rotated 90° clockwise, then

`(x,y)\rightarrow (y,-x)`

If a point reflects across the line y=-x, then

`(x,y)\rightarrow (-y,-x)`

Answer 2

D. (x, y) → (-x, -y)

Explanation:

A. (x,y) → (y,x) . . . . reflects across the line y=x

B. (x,y) → (y,-x) . . . . rotates 90° CCW

C. (x,y) → (-y,-x) . . . . reflects across the line y=-x

D. (x,y) → (-x,-y) . . . . rotates 180° about the origin