Question

An electron is released from rest in a uniform electric field of 418 N/C near a particle detector. The electron arrives at the detector with a speed of 3.70 x 106 m/s (a) What was the uniform acceleration of the electron? (Enter the magnitude.) m/s (b) How long did the electron take to reach the detector? (c) What distance was traveled by the electron? cm (d) What is the kinetic energy of the electron when it reaches the detector?

Answer 1

a) 7.35 x 10¹³ m/s²

b) 5.03 x 10⁻⁸ sec

c) 9.3 cm

d) 6.23 x 10⁻¹⁸ J

Step-by-step explanation:

E = magnitude of electric field = 418 N/C

q = magnitude of charge on electron = 1.6 x 10⁻¹⁹ C

m = mass of the electron = 9.1 x 10⁻³¹ kg

a)

acceleration of the electron is given as

`a = (qE)/(m)`

`a = ((1.6* 10^(-19))(418))/((9.1* 10^(-31)))`

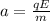
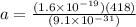
a = 7.35 x 10¹³ m/s²

b)

v = final velocity of the electron = 3.70 x 10⁶ m/s

v₀ = initial velocity of the electron = 0 m/s

t = time taken

Using the equation

v = v₀ + at

3.70 x 10⁶ = 0 + (7.35 x 10¹³) t

t = 5.03 x 10⁻⁸ sec

c)

d = distance traveled by the electron

using the equation

d = v₀ t + (0.5) at²

d = (0) (5.03 x 10⁻⁸) + (0.5) (7.35 x 10¹³) (5.03 x 10⁻⁸)²

d = 0.093 m

d = 9.3 cm

d)

Kinetic energy of the electron is given as

KE = (0.5) m v²

KE = (0.5) (9.1 x 10⁻³¹) (3.70 x 10⁶)²

KE = 6.23 x 10⁻¹⁸ J