Answer : The activation energy for the reaction is, 1.151 KJ
Explanation :
According to the Arrhenius equation,
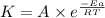
or,
![\log ((K_2)/(K_1))=(Ea)/(2.303* R)[(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/n4xcj74485qvk235cd8fhqu0rg9bb3z2n1.png)
where,
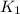 = rate constant at
= rate constant at
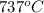 =
=
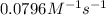
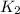 = rate constant at
= rate constant at
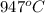 =
=
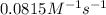
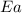 = activation energy for the reaction = ?
= activation energy for the reaction = ?
R = gas constant = 8.314 J/mole.K
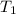 = initial temperature =
= initial temperature =
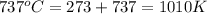
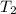 = final temperature =
= final temperature =
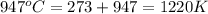
Now put all the given values in this formula, we get:
![\log ((0.0815M^(-1)s^(-1))/(0.0796M^(-1)s^(-1)))=(Ea)/(2.303* 8.314J/mole.K)[(1)/(1010K)-(1)/(1220K)]](https://img.qammunity.org/2020/formulas/chemistry/college/3prm6d3lwnmtsiu3ig2ukbrejvdx9wfn30.png)
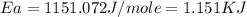
Therefore, the activation energy for the reaction is, 1.151 KJ