Answer:
all numbers greater than or equal to -1
Explanation:
Let's find the vertex.
Since the function is in factored form, I'm going to find the zeros.
The average of the zeros will give me the x-coordinate of the vertex.
I can then find the y-coordinate of the vertex by using the equation
y=(x-4)(x-2).
Also the parabola is open up since the coefficient of x^2 is positive (or 1 in this case).
So the range has something to do with the y's. It is where the function exist for the y-values.
So the range for this one since the parabola is open up will be of the form
[y-coordinate of vertex , infinity).
So let's begin.
The zeros can found by solving (x-4)(x-2)=0.
This means we need to solve both x-4=0 and x-2=0.
x-4=0 gives us x=4
x-2=0 gives us x=2
Now the average of our x-intercepts (or zeros) is (4+2)/2=6/2=3.
So the x-coordinate of the vertex is 3. To find the y-coordinate of the vertex we are going to use y=(x-4)(x-2) where x=3.
Plug in: y=(3-4)(3-2)=(-1)(1)=-1.
So the range is
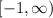
or all numbers greater than or equal to -1