Answer:
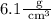
Explanation:
We have been given that mass of an irregular object is 1220 g and it displaces 200 cubic cm of water when placed in a large overflow container. We are asked to find density of the object.
We will use density formula to solve our given problem.
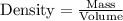
Since the object displaces 200 cubic cm of water, so the volume of irregular object will be equal to 200 cubic cm.
Upon substituting our given values in density formula, we will get:
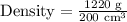
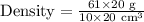
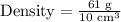
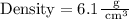
Therefore, the density of the irregular object will be 6.1 grams per cubic centimeters.