Question

An object is hung on the end of a vertical spring and is released from rest with the spring 3 unstressed. If the object falls 3.42 cm before first coming to rest, find the period of the resulting oscillatory motion

Answer 1

The period of the resulting oscillatory motion is 0.20 s.

Step-by-step explanation:

Given that,

Spring constant
`k= 3\ N/m^2`

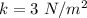
We need to calculate the time period

The object is at rest and has no elastic potential but it does has gravitational potential.

If the object falls then the the gravitational potential change in to the elastic potential.

So,

`mgh=(1)/(2)kh^2`

`m=(1)/(2)*(kh)/(g)`

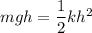
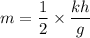
Where,h = distance

k = spring constant

Put the value into the formula

`m=(1*3*3.42*10^(-2))/(2*9.8)`

`m=5.235*10^(-3)\ kg`

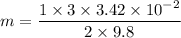
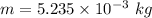
Using formula of time period

`T=(1)/(2\pi)*\sqrt{(m)/(k)}`

Put the value into the formula

`T=(1)/(2\pi)*\sqrt{(5.235*10^(-2))/(3)}`

`T=0.20\ sec`

Hence, The period of the resulting oscillatory motion is 0.20 s.