Question

An aluminium alloy used for making cans is cold rolled into a strip of thickness 0.3mm and width 1m. It is coiled round a drum of diameter 15cm, and the outer diameter of the coil is 1m. In the cold rolled condition, the dislocation density is approximately 1015 m-2. Estimate: (i) The mass of aluminium on the coil; (ii) The total length of strip on the coil; (iii) The total length of dislocation in the coiled strip.

Answer 1

1. Mass = 2070 kg

2.Total length of strip = 2556 m

3. Total length of dislocation = 7.67 X
`10^(14)` m

Step-by-step explanation:

Given:

Aluminium coil thickness, t = 0.3 mm

= 0.3 X
`10^(-3)` m

Width of the coil,w = 1 m

Drum diameter, d = 15 cm

= 0.15 m

Coil outer diameter, d = 1 m

Dislocation density =
`10^(15)`
`m^(2)`

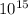
1). Area of the coil, A =
`(\pi )/(4)*` (
`d_(coil) ^(2)`-
`d_(drum) ^(2)`)

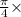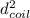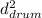A =
`(\pi )/(4)* (1^(2)-0.15^(2))`

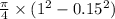
A = 0.767
`m^(2)`

Volume of the coil,V = A X w

= 0.767 X 1

= 0.767
`m^(3)`

We know density of aluminum at STP = 2.7 X
`10^(3)`

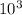
Therefore, mass of the aluminum coil is,

Mass,m = Density of aluminium X Volume

= 2.7 X
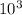`10^(3)` X 0.767

= 2070 kg

Mass = 2070 kg

2). Total length of trip of coil is given by

L = Volume of coil / area of strip

=
`(0.767)/(1* 0.3* 10^(-3))`

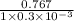
= 2556 m

Total length of strip = 2556 m

3). Total length of dislocation of the coiled strip = volume X dislocation density

= 0.767 X
`10^(15)`

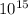
= 7.67 X
`10^(14)`

Total length of dislocation = 7.67 X
`10^(14)` m