Question

Which equations represent the line that is parallel to 3x − 4y = 7 and passes through the point (−4, −2)? Select two options.

Options:
1. y= -3/4x+1
2. 3x-4y=-4
3.4x-3y=-3
4. y-2=-3/4(x-4)
5. y+ 2 = 3/4(x + 4)

Please help ASAP thank you ! :)

Answer 1

OPTION 2.

OPTION 5.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the line
`3x - 4y = 7`, solve for "y":

`3x - 4y = 7\\\\-4y=-3x+7\\\\y=(3)/(4)x-(7)/(4)`

The slope of this line is:

`m=(3)/(4)`

Since the slopes of parallel lines are equal, the slope of the other line is:

`m=(3)/(4)`

Substitute the slope and the given point into
`y=mx+b` and solve for "b":

`-2=(3)/(4)(-4)+b\\\\-2+3=b\\\\b=1`

Then, the equation of this line in Slope-Intercept form is:

`y=(3)/(4)x+1`

The equation of the line in Standard form is:

`Ax+By=C`

Then, manipulating the equation
`y=(3)/(4)x+1` algebraically, we get:

`y-1=(3)/(4)x\\\\4(y-1)=3x\\\\4y-4=3x\\\\-4=3x-4y\\\\3x-4y=-4`

Answer 2

2 and 5

Explanation:

The slope-intercept form of a line is y=mx-b where m is slope and b is y-intercept.

The point-slope form of a line is y-y1=m(x-x1) where m is the slope and (x1,y1) is a point on the line.

The standard form a line is ax+by=c.

So anyways parallel lines have the same slope.

So if we are looking for a line parallel to 3x-4y=7 then we need to know the slope of this line so we can find the slope of our parallel line.

3x-4y=7

Goal: Put into slope-intercept form

3x-4y=7

Subtract 3x on both sides:

-4y=-3x+7

Divide both sides by -4:

`y=(-3)/(-4)x+(7)/(-4)`

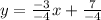
Simplify:

`y=(3)/(4)x+(-7)/(4)`

So the slope of this line is 3/4. So our line that is parallel to this one will have this same slope.

So we know our line should be in the form of
`y=(3)/(4)x+b`.

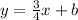To find b we will use the point that is suppose to be on our new line here which is (x,y)=(-4,-2).

So plugging this in to solve for b now:

`-2=(3)/(4)(-4)+b`

`-2=-3+b`

`3-2=b`

`b=1`

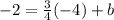
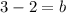
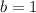
so the equation of our line in slope-intercept form is
`y=(3)/(4)x+1`

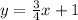
So that isn't option 1 because the slope is different. That was the only option that was in slope-intercept form.

The standard form of a line is ax+by=c and we have 2 options that look like that.

So let's rearrange the line that we just found into that form.

`y=(3)/(4)x+1`

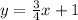
Clear the fractions because we only want integer coefficients by multiplying both sides by 4.

This gives us:

`4y=3x+4`

Subtract 3x on both sides:

`-3x+4y=4`

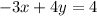
I don't see this option either.

Multiply both sides by -1:

`3x-4y=-4`

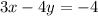
I do see this as a option. So far the only option that works is 2.

Let's look at point slope form now.

We had the point that our line went through was (x1,y1)=(-4,-2) and the slope,m, was 3/4 (we found this earlier).

y-y1=m(x-x1)

Plug in like so:

y-(-2)=3/4(x-(-4))

y+2=3/4 (x+4)

So option 5 looks good too.