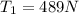Question

A window washer is standing on a scaffold supported by a vertical rope at each end. The scaffold welghs 198 N and is 3.2 m long. what is the tension in each rope whien the 6oo-N worker stands 1.12 m from one end? smaller tension arger tension

Answer 1

`T_2 = 309 N`

`T_1 = 489 N`

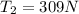
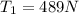
Step-by-step explanation:

As we know that total tension in both the ropes is counter balancing the weight of scaffold and worker both

so here we will have

`T_1 + T_2 = (m + M)g`

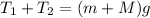
now we have

`T_1 + T_2 = 198 + 600 = 798 N`

now we also know that net torque due to both tension force in the string with respect to the position of worker must be zero so that platform will remain in equilibrium and horizontal in position

so here we will have

`T_1(1.12) + (198)(1.6 - 1.12) = T_2(3.2 - 1.12)`

`T_1+ 84.86 = 1.86 T_2`

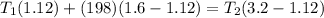
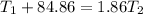
now from above two equations we will have

`(1.86 T_2 - 84.86) + T_2 = 798`

`T_2 = 309 N`

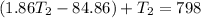
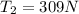
also we have

`T_1 = 489 N`