Question

Air is compressed by a compressor from v1 = 1.0 m3/kg to v2 = 0.71 m3/kg in a reversible, isothermal process. The air temperature is maintained constant at 25 oC during this process as a result of heat transfer to the surroundings. Air moves through the compressor at a rate of m = 1 kg/s. a)- Determine the entropy change of the air per kg of air. b)- What is the power required by the compressor? c)- What is the rate at which entropy leave the compressor?

Answer 1

(a)
`s_2-s_1`= -0.098 KJ/kg-K

(b)P= 29.8 KW

(c)
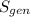`S_(gen)`= -0.098 KW/K

Step-by-step explanation:

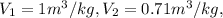`V_1=1m^3/kg,V_2=0.71m^3/kg,` mass flow rate= 1 kg/s.

T=25°C

Air treating as ideal gas

(a)

We know that entropy change for ideal gas between two states

`s_2-s_1=mC_v\ln (T_2)/(T_1)+mR\ln (V_2)/(V_1)`

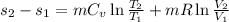
Given that this is isothermal process so

`s_2-s_1=mR\ln (V_2)/(V_1)`

`s_2-s_1=1* 0.287\ln (0.71)/(1)`

`s_2-s_1`= -0.098 KJ/kg-K

(b)

Power required

`P=\dot{m}T\Delta S`

`P=1* (273+25)(s_2-s_1)`

`P=1* (273+25)(-0.098)`

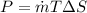
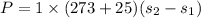
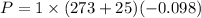
P= -29.8 KW (Negative sign means it is compression process.)

(c)

Rate of entropy generation
`S_(gen)`

`S_(gen)=\dot{m}T\Delta S`

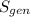
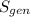`S_(gen)`=1(-0.098)

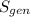`S_(gen)`= -0.098 KW/K