Question

a wave travels in a string at 58 m/s. a second string of 10% greater linear density has the same tension applied as in the first string. what will be the resulting wave speed in the second string

Answer 1

The speed of wave in the second string is 55.3 m/s.

Step-by-step explanation:

Given that,

Speed of wave in first string= 58 m/s

We need to calculate the wave speed

Using formula of speed for first string

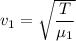`v_(1)=\sqrt{(T)/(\mu_(1))}`...(I)

For second string

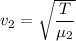`v_(2)=\sqrt{(T)/(\mu_(2))}`...(II)

Divided equation (II) by equation (I)

`(v_(2))/(v_(1))=\sqrt{((T)/(\mu_(2)))/((T)/(\mu_(1)))}`

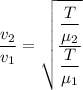
Here, Tension is same in both string

So,

`(v_(2))/(v_(1))=\sqrt{(\mu_(1))/(\mu_(2))}`

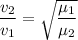
The linear density of the second string

`\mu_(2)=\mu_(1)+(10)/(100)\mu_(1)`

`\mu_(2)=(110)/(100)\mu_(1)`

`\mu_(2)=1.1\mu_(1)`

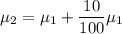
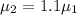
Now, Put the value of linear density of second string

`(v_(2))/(v_(1))=\sqrt{(\mu_(1))/(1.1\mu_(1))}`

`v_(2)=v_(1)*\sqrt{(1)/(1.1)}`

`v_(2)=58*\sqrt{(1)/(1.1)}`

`v_(2)=55.3\ m/s`

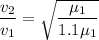
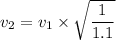
Hence, The speed of wave in the second string is 55.3 m/s.