Question

Two points on L1 and two points on L2 are given. Use the slope formula to determine if lines L1 and L2 are parallel, perpendicular, or neither.

L1: (1, 10) and (-1, 7)
L2: (0, 3) and (1, 5 )

Answer 1

The lines L1 and L2 neither parallel nor perpendicular

Explanation:

* Lets revise how to find a slope of a line

- If a line passes through points (x1 , y1) and (x2 , y2), then the slope

of the line is
`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

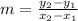
- Parallel lines have same slopes

- Perpendicular lines have additive, multiplicative slopes

( the product of their slopes is -1)

* Lets solve the problem

∵ L1 passes through the point (1 , 10) and (-1 , 7)

- Let (1 , 10) is (x1 , y1) and (-1 , 7) is (x2 , y2)

∴ x1 = 1 , x2 = -1 and y1 = 10 , y2 = 7

∴ The slope of L1 is
`m1 = (7-10)/(-1-1)=(-3)/(-2)=(3)/(2)`

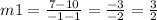
∵ L2 passes through the point (0 , 3) and (1 , 5)

- Let (0 , 3) is (x1 , y1) and (1 , 5) is (x2 , y2)

∴ x1 = 0 , x2 = 1 and y1 = 3 , y2 = 5

∴ The slope of L2 is
`m2=(5-3)/(1-0)=(2)/(1)=2`

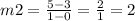
∵ m1 = 3/2 and m2 = 2

- The two lines have different slopes and their product not equal -1

∴ The lines L1 and L2 neither parallel nor perpendicular