Answer:
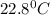
Explanation:-
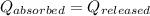
As we know that,
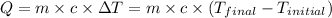
![m_1* c* (T_(final)-T_1)=-[m_2* c* (T_(final)-T_2)]](https://img.qammunity.org/2020/formulas/physics/college/jimhrvet2ab55e8azsefjq8pz22nqyihiz.png)
where,
 = mass of iron horseshoe = 0.35 kg = 350 g (1kg=1000g[/tex]
= mass of iron horseshoe = 0.35 kg = 350 g (1kg=1000g[/tex]
 = mass of water = 21.9 kg = 21900 g
= mass of water = 21.9 kg = 21900 g
 = final temperature = ?
= final temperature = ?
 = temperature of iron horseshoe =
= temperature of iron horseshoe =
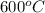
 = temperature of water =
= temperature of water =
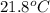
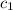 = specific heat of iron horseshoe =
= specific heat of iron horseshoe =
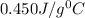
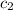 = specific heat of water =
= specific heat of water =
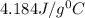
Now put all the given values in equation (1), we get
![m_1* c_1* (T_(final)-T_1)=-[m_2* c_2* (T_(final)-T_2)]](https://img.qammunity.org/2020/formulas/chemistry/college/bm2kxludvecqgwsul6e5upktie71evfnq2.png)
![350* 0.450* (T_(final)-600)^0C=-[21900g* 4.184* (T_(final)-21.8)]](https://img.qammunity.org/2020/formulas/physics/college/1xop4huk3yo7xd2myqyz3deufqgirt4snh.png)
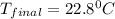
Therefore, the final equilibrium temperature is
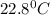 .
.