Question

Two identical loudspeakers are some distance apart. A person stands 5.20 m from one speaker and 4.10 m from the other. What is the third lowest frequency at which destructive interference will occur at this point? The speed of sound in air is 344 m/s.

Answer 1

125.09 Hz

Step-by-step explanation:

Given : A person stands 5.20 from one speaker and 4.10 m away from the other speaker.

Distance between the speakers is 5.20 - 4.10 =1.10 m

We know that

For destructive interferences

n . λ / 2

where n =1,3,5,7....

Therefore difference between the speakers is

5.10 - 4.20 = 1 X 0.5 λ

λ = 2.2

Given velocity of sound is V = 344 m/s

Therefore frequency, f =
`(v)/(\lambda )`

=
`(344)/(2.2 )`

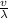
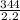
= 156.36 Hz

Now, the third lowest frequency is given by

λ = (5.20-4.10) X 5 X 0.5

= 2.75 m

Therefore frequency, f =
`(v)/(\lambda)`

=
`(344)/(2.75)`

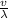
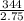
= 125.09 Hz

Therefore third lowest frequency is 125.09 Hz