Question

A pendulum has an oscillation frequency (T) which is assumed to depend upon its length (L), load mass (m) and the acceleration of gravity (g). Determine the relationship between oscillation frequency, length, load mass and acceleration of gravity. Differentiate as well which variable does not affect the oscillation frequency.

Answer 1

Mass does not affect oscillation frequency.

Explanation:

Let the bob of the pendulum makes a small angular displacement θ. When the pendulum is displaced from the equilibrium position, a restoring force tries to act upon it and it tries to bring the pendulum back to its equilibrium position. Let this restoring force be F.

Therefore, F = -mgsinθ

Now for pendulum, for small angle of θ,

sinθ
`\simeq`θ

Therefore, F = -mgθ

Now from Newton's 2nd law of motion,

F = m.a = -mgθ

`\Rightarrow m.(d^(2)x)/(dt^(2)) = - mg\Theta`

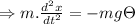
Now since, x = θ.L

`\Rightarrow L.(d^(2)\Theta )/(dt^(2))= -g\Theta`

`\Rightarrow (d^(2)\Theta )/(dt^(2))= -(g)/(L).\Theta`

`\Rightarrow (d^(2)\Theta )/(dt^(2))+(g)/(L).\Theta =0`

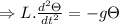
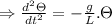
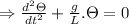
Therefore, angular frequency

`\omega ^(2)` =
`(g)/(L)`

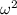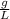
ω =
`\sqrt{(g)/(L)}`

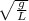
Also we know angular frequency is , ω = 2.π.f

where f is frequency

Therefore

2πf =
`\sqrt{(g)/(L)}`

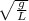
f =
`(1)/(2 \pi )\sqrt{(g)/(L)}`

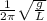
So from here we can see that frequency,f is independent of mass, hence it does not affect frequency.