Question

Determine Whether the following function is even, odd, or neither

f(x) = x^4 + 7x^2 - 30

Answer 1

even

Explanation:

f(-x)=f(x) means f is even

f(-x)=-f(x) means f is odd

If you get neither f(x) or -f(x), you just say it is neither.

f(x)=x^4+7x^2-30

f(-x)=(-x)^4+7(-x)^2-30

f(-x)=x^4+7x^2-30

f(-x)=f(x)

so f is even.

Notes:

(-x)^even=x^even

(-x)^odd=-(x^odd)

Examples (-x)^88=x^88 and (-x)^85=-(x^85)

Answer 2

Answer: even

Explanation:

By definition a function is even if and only if it is fulfilled that:

`f(-x) = f(x)`

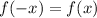
By definition, a function is odd if and only if it is true that:

`f (-x) = -f(x)`

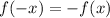
Then we must prove the parity for the function:
`f(x) = x^4 + 7x^2 - 30`

`f(-x) = (-x)^4 + 7(-x)^2 - 30`

`f(-x) = x^4 + 7x^2 - 30=f(x)`

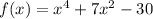
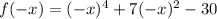
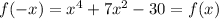
Note that for this case it is true that:
`f(-x) = f(x)`

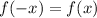
Finally the function is even