Answer:
Maximum shear stress is 11.47 MPa.
Step-by-step explanation:
Given:
D=.75 in⇒D=19.05 mm
P=7 hp⇒ P=5219.9 W
N=3200 rpm
We know that
P=T
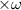
Where T is the torque and
 is the speed of shaft.
is the speed of shaft.
P=
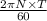
So 5219.9=

T=15.57 N-m
We know that maximum shear stress in shaft
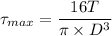
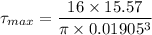
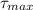 =11.47 MPa
=11.47 MPa
So maximum shear stress is 11.47 MPa.