Question

A singly charged ion of 7Li (an isotope of lithium which lost only one electron) has a mass of 1.16 ×10^-26 kg. It is accelerated through a potential difference of 224 V and then enters a magnetic field with magnitude 0.724 T perpendicular to the path of the ion. What is the radius of the ion’s path in the magnetic field? (Give your answer in decimal using "mm"(millimeter) as unit)

Answer 1

Step-by-step explanation:

It is given that,

Mass of lithium,
`m=1.16* 10^(-26)\ kg`

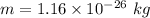
It is accelerated through a potential difference, V = 224 V

Uniform magnetic field, B = 0.724 T

Applying the conservation of energy as :

`(1)/(2)mv^2=qV`

`v=\sqrt{(2qV)/(m)}`

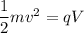
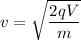
q is the charge on an electron

`v=\sqrt{(2* 1.6* 10^(-19)\ C* 224\ V)/(1.16* 10^(-26)\ kg)}`

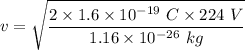
v = 78608.58 m/s

`v=7.86* 10^4\ m/s`

To find the radius of the ion's path in the magnetic field. The centripetal force is balanced by the magnetic force as :

`qvB=(mv^2)/(r)`

`r=(mv)/(qB)`

`r=(1.16* 10^(-26)\ kg* 7.86* 10^4\ m/s)/(1.6* 10^(-19)\ C* 0.724\ T)`

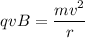
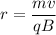
r = 0.0078 meters

So, the radius of the path of the ion is 0.0078 meters. Hence, this is the required solution.