Answer:
a=192
b=96
c=64
d=48
Explanation:
So we have
 where
where
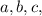 and
and
 are integers.
are integers.
We also have
 and
and
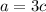 and
and
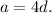
 means
means
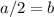
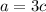 means
means
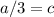
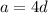 means
means
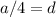
Let's plug those in:

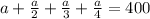
Multiply both sides by 4(3)=12 to clear the fractions:
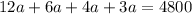
Combine like terms:
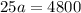
Divide both sides by 25:

Simplify:
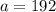 .
.
Let's go back and find
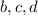 now.
now.
b is half of a so half of 192 is 96 which means b=96
c is a third of a so a third of 192 is 64 which means c=64
d is a fourth of a so a fourth of 192 is 48 which means d=48
So
a=192
b=96
c=64
d=48