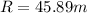Question

A projectile launcher is loaded by providing an average force of 23 N to compress a spring 12 cm. If the projectile has a mass of 5.7 grams and is shot at an angle of 57 degrees at a height of 1.37 meters above the floor, what is the spring constant of the launcher, muzzle velocity of the ball, time in the air, maximum height and horizontal distance travelled?

Answer 1

a) k = 191.67 N\m

b) V = 22 m/s

c) t = 3.83s

d) 17.36m

e) 45.89 m

Step-by-step explanation:

given:

F = 23 N

x = 12 cm = 0.12 m

mass of projectile, m = 5.7g = 5.7×10⁻³ kg

a) For a spring

F = kx

where,

F = Applied force

k = spring constant

x = change in in spring length

thus, we have

23 = k×0.12

or

k = 23/0.12

⇒ k = 191.67 N\m

b) From the conservation of energy between the start and the point of interest we have

`(1)/(2)* kx^(2)=(1)/(2)mV^(2)`

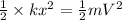
where,

V = velocity of the projectile at 1.37 m above the floor

`(1)/(2)* 191.67* 0.12^(2)=(1)/(2)5.7* 10^(-3)V^(2)`

V = 22 m/s

c) time in air (t)

applying the Newtons's equaton of motion

`h = Vsin\Theta*  t +(1)/(2)a_(y)t^(2)`

substituting the values in the above equation we get

`-1.37 = 22sin57^(\circ) *  t +(1)/(2)(-9.8)t^(2)`

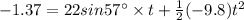
or

`4.9t^(2)-18.45t-1.37 = 0`

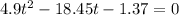
solving the qudratic equation for 't', we get

t = 3.83s

d) For maximum height (
`H_(max)`)

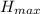we have from the equations of projectile motion

`H_(max) =(V^(2)sin^(2)\theta )/(2g)`

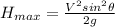
substituting the values in the above equation we get

`H_(max) =(22^(2)sin^(2)57^(\circ) )/(2* 9.8)`

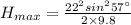
or

`H_(max) =17.36 m`

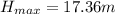
the height with respect to the ground surface will be = 17.36m + 1.37 m 18.73m

e)For horizontal distance traveled (R) we have the formula

`R = Vcos\theta* t`

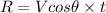
substituting the values in the above equation we get

`R =22* cos57^(\circ) * 3.83`

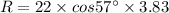
or

`R =45.89 m`