Answer:
The no of revolutions is 2.032 revolution.
Step-by-step explanation:
Given that,
Moment of inertia = 0.85 Kgm²
Radius = 170 mm
Force = 32 N
Time = 2s
We need to calculate the angular acceleration
Using formula of torque
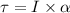
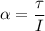

Where, F = force
r = radius
I = moment of inertia
Put the value into the formula
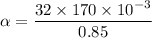
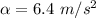
We need to calculate the rotational speed
Using equation of angular motion
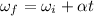
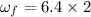

We need to calculate the angular position
Using equation of angular motion


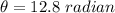
We need to calculate no of revolutions
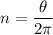
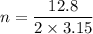
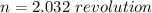
Hence, The no of revolutions is 2.032 revolution.