Question

Tracey pays $18 to enter a theme park, plus $2 for each ride. Which of the following correctly describes the slope? A. she must pay a flat rate of $18. B. Her total cost increases by $2, for each ride purchased. C. Her total cost is at least $20. D. her total cost increased by $3, for each ride purchased

Answer 1

B.

Explanation:

You pay a one time fee of 18 dollars and then 2 dollars per ride.

The expression for that is 18+2r where r represents the number of rides and the output of (18+2r) is amount you spend.

f(r)=2r+18 when compared to f(x)=mx+b where m is slope and b is y-intercept

you should see that the slope is $2 per ride.

B. is the option that says this.

Answer 2

Answer: Option B

Her total cost increases by $2, for each ride purchased

Explanation:

We know that $ 18 is the cost of the ticket. We do not know exactly how many trips you will make, but we know that the cost is $ 2 for each ride.

If we call "x" the number of rides then we know that the total cost "y" is:

`y = 2x + 18`

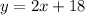
Note that the cost increases by $2 for each ride

The equation of a line has the following form

`y = mx + b`

Where m is the slope of the line.

In this case we have the following equation

`y = 2x + 18`

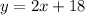
Therefore
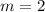`m = 2`. Then the slope is the cost of $2 for each ride

Finally the answer is the option B. Her total cost increases by $2, for each ride purchased