Question

A rod of 2.0-m length and a square (2.0 mm x 2.0 mm) cross section is made of a material with a resistivity of 6.0 x 10^-8 0.Ω.m. If a potential difference of 0.50 V is placed across the ends of the rod, at what rate is heat generated in the rod?

Answer 1

Heat generated in the rod is 8.33 watts.

Step-by-step explanation:

It is given that,

Length of rod, l = 2 m

Area of cross section,
`A=2\ mm* 2\ mm=4\ mm^2=4* 10^(-6)\ m^2`

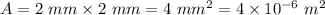
Resistivity of rod,
`\rho=6* 10^(-8)\ \Omega-m`

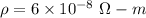
Potential difference, V = 0.5 V

The value of resistance is given by :

`R=\rho(l)/(A)`

`R=6* 10^(-8)\ \Omega-m* (2\ m)/(4* 10^(-6)\ m^2)`

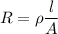
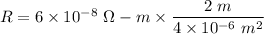
R = 0.03 ohms

Let H is the rate at which heat is generated in the rod . It is given by :

`(H)/(t)=I^2R`

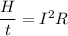
Since,
`I=(V)/(R)`

`(H)/(t)=(V^2)/(R)`

`(H)/(t)=((0.5)^2)/(0.03)`

`(H)/(t)=8.33\ watts`

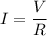
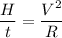
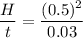
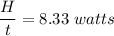
So, the at which heat is generated in the rod is 8.33 watts. Hence, this is the required solution.