Question

A given binomial experiment has n=100 trials and p=1/3. Is it more likely to get x=20 successes or x=45 successes. Why?

Answer 1

The P(x=45) is more that the P(x=20). Therefore x=45 successes is more likely to get.

Explanation:

Given information: n=100 and p=1/3.

According to the binomial distribution, the probability of getting r success in n trials is

`P(x=r)=^nC_rp^rq^(n-r)`

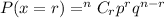
where, n is total trials, p is probability of success and q is probability of failure.

Total trials, n = 100

Probability of success, p =
`(1)/(3)`

Probability of failure, q =
`1-(1)/(3)=(2)/(3)`

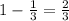
The probability of 20 successes is

`P(x=20)=^(100)C_(20)* ((1)/(3))^(20)* ((2)/(3))^(100-20)`

`P(x=20)=(100!)/(20!(100-20)!)* ((1)/(3))^(20)* ((2)/(3))^(80)\approx 0.001257`

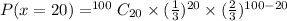
The probability of 45 successes is

`P(x=45)=^(100)C_(45)* ((1)/(3))^(45)* ((2)/(3))^(100-45)`

`P(x=45)=(100!)/(45!(100-45)!)* ((1)/(3))^(45)* ((2)/(3))^(55)\approx 0.004296`

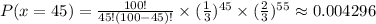
The P(x=45) is more that the P(x=20). Therefore x=45 successes is more likely to get.