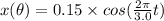Answer:
a)
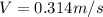
b)
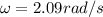
c)
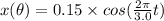
Step-by-step explanation:
Given:
Radius of the circle, r = 15cm = 0.15m
Time period, T =3.0s
a) The velocity (V) of a particle moving in the circular motion is given as:
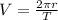
substituting the given values in the above equation we get
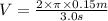
or
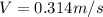
b) Angular speed (
 ) is given as:
) is given as:
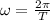
or
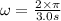
or
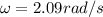
c) The position of the particle on the x-position is given as:
 (reffer the attached figure)
(reffer the attached figure)
now the relation between the Θ and the time T is given as:
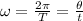
or
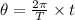
or

substituting the values of r and Θ, we get