Question

A disk brake has two pads which cover 45 degrees of the disk. The outside radius is 6.0 inch and the inside radius is 4.0 inch. Assume a coefficient of friction of 0.4, and a max pressure, pa=100 psi. a) Find the force required to apply one pad. b) Find the torque capacity for both pads.

Answer 1

f = 628.32 lb

t = 2513.28 lb-inc

Step-by-step explanation:

given data:

θ = 45°

outside radius = 6 inch

inside radius = 4 inch

coefficient of friction = 0.4

max pressure = 100 psi

a) determine force required for applying one pad

f =
`(\theta )/(360)* 2\pi *p_(max)*r_(i)(r_(o)-r_(i))`

f =
`(45 )/(360)* 2\pi *100*4(6-4)`

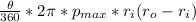
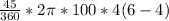
f = 628.32 lb

b) torque capacity (t)

t =
`\mu *f*r_(average)^{}`

t = 0.4 *628.32*5

torque = 1256.64 lb-inc

for both pad = 2 * 1256.64 =2513.28 lb-inc