Question

A flywheel in the form of a uniformly thick disk of radius 1.93 m has a mass of 92.1 kg and spins counterclockwise at 419 rpm. Calculate the constant torque required to stop it in 1.25 min.

Answer 1

Torque = 99.48 N-m²

Step-by-step explanation:

It is given that,

Radius of the flywheel, r = 1.93 m

Mass of the disk, m = 92.1 kg

Initial angular velocity,
`\omega_i=419\ rpm=43.87\ rad/s`

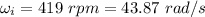
Final angular speed,
`\omega_f=0`

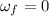
We need to find the constant torque required to stop it in 1.25 min, t = 1.25 minutes = 75 seconds

Torque is given by :

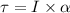`\tau=I* \alpha`...........(1)

I is moment of inertia, for a solid disk,
`I=(mr^2)/(2)`

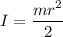
`\alpha` is angular acceleration

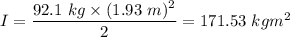`I=(92.1\ kg* (1.93\ m)^2)/(2)=171.53\ kgm^2`..............(2)

Now finding the value of angular acceleration as :

`\omega_f=\omega_i+\alpha t`

`0=43.87+\alpha * 75`

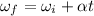
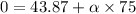
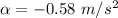`\alpha =-0.58\ m/s^2`..........(3)

Using equation (2) and (3), solve equation (1) as :

`\tau=171.53\ kgm^2* -0.58\ m/s^2`

`\tau=-99.48\ N-m^2`

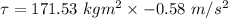
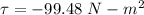
So, the torque require to stop the flywheel is 99.48 N-m². Hence, this is the required solution.