Answer:
Torque = 99.48 N-m²
Step-by-step explanation:
It is given that,
Radius of the flywheel, r = 1.93 m
Mass of the disk, m = 92.1 kg
Initial angular velocity,
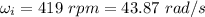
Final angular speed,

We need to find the constant torque required to stop it in 1.25 min, t = 1.25 minutes = 75 seconds
Torque is given by :
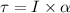 ...........(1)
...........(1)
I is moment of inertia, for a solid disk,
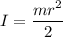
 is angular acceleration
is angular acceleration
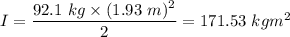 ..............(2)
..............(2)
Now finding the value of angular acceleration as :
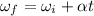
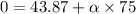
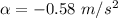 ..........(3)
..........(3)
Using equation (2) and (3), solve equation (1) as :
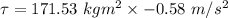
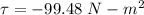
So, the torque require to stop the flywheel is 99.48 N-m². Hence, this is the required solution.