Question

Working together, two secretaries can stuff the envelopes for a political fund-raising letter in 3 hours. Working alone, it takes the slower worker 8 hours longer to do the job than the faster worker. How long does it take each to do the job alone?

Answer 1

To solve this work rate problem, we set up an equation with combined work rates and find that the faster worker takes 3 hours alone, while the slower worker takes 11 hours alone.

Step-by-step explanation:

The question states that two secretaries can stuff envelopes together in 3 hours. The slower worker takes 8 hours more than the faster worker to complete the job alone. To find how long it takes each secretary to complete the job alone, we can set up an equation using the reciprocal of their work rates.

Let x be the time it takes for the faster worker to stuff the envelopes alone. Then, the slower worker will take x + 8 hours. The work rate of the faster worker is 1/x and the slower worker's rate is 1/(x + 8). Working together, their combined work rate is 1/3 per hour (since they complete the task in 3 hours).

The combined work rate equation will be:

1/x + 1/(x + 8) = 1/3

To solve this equation:

1. Multiply every term by the common denominator, which is 3x(x + 8).
2. This gives us 3(x + 8) + 3x = x(x + 8).
3. Simplify and solve the resulting quadratic equation.
4. This results in x² + 8x - 3x - 24 = 0, which simplifies to x² + 5x - 24 = 0.
5. Factor the quadratic equation to find the values of x.
6. The factors of 24 that add up to 5 are 8 and -3, so (x + 8)(x - 3) = 0.
7. Therefore, x = 3 or x = -8. Since time cannot be negative, we disregard x = -8.
8. The faster worker takes 3 hours and the slower worker takes 3 + 8 = 11 hours.

As a result, the faster worker takes 3 hours to complete the job alone, and the slower worker takes 11 hours to complete the job alone.

Answer 2

Faster worker takes 4 hours and slower worker takes 12 hours.

Step-by-step explanation:

Let x be the time ( in hours ) taken by faster worker,

So, according to the question,

Time taken by slower worker = (x+8) hours,

Thus, the one day work of faster worker =
`(1)/(x)`

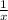
Also, the one day work of slower worker =
`(1)/(x+8)`

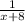
So, the total one day work when they work together =
`(1)/(x)+(1)/(x+8)`

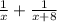
Given,

They take 3 hours in working together,

So, their combined one day work =
`(1)/(3)`

`\implies (1)/(x)+(1)/(x+8)=(1)/(3)`

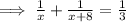
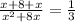`(x+8+x)/(x^2+8x)=(1)/(3)` ( Adding fractions )

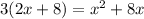`3(2x+8)=x^2+8x` ( Cross multiplication )

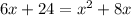`6x+24=x^2+8x` ( Distributive property )

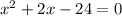`x^2+2x-24=0` ( Subtraction property of equality )

By quadratic formula,

`x=(-2\pm √(100))/(2)`

`x=(-2\pm 10)/(2)`

`\implies x=4\text{ or }x=-6`

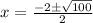
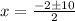
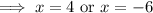
Since, hours can not negative,

Hence, time taken by faster worker = x hours = 4 hours,

And, the time taken by slower worker = x + 8 = 12 hours.