Question

Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After 9 hours of burning, a candle has a height of 17.5 centimeters. After 24 hours of burning, its height is 22 centimeters. What is the height of the candle after 22 hours?

Answer 1

The candle has a height of 21.4 cm after burning for 22 hours.

Explanation:

let x=hours, m=rate of change, and y= candle height

First you have to find the slope or, rate of change using the slope formula. y2-y1 divided by x2-x1 .

Here is our points (9, 17.5) and (24, 22)

x1 y1 x2 y2

Now we put these into the equation and solve

`(22-17.5)/(24-9)` =
`(3)/(10)`

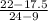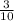
Now that we have the slope of 3/10 we can use this to find the y-intercept using the point-slope equation.

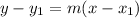`y-y_(1) =m(x-x_(1) )` y-17.5= .3(x-9) Solve

y-17.5=.3x-2.7 y -14.8= .3x

+2.7 +2.7 +14.8 +14.8

y=.3x+14.8 the y-intercept is 14.8

Now we use this equation to plug in the 22 hours.

y=.3(22) +14.8

y=6.6+14.8

y= 21.4 The candle has a height of 21.4 cm after burning for 22 hours.