Question

A golf ball was thrown with a speed of 25 m/sec at an angle of 65° above the horizontal. What is the horizontal distance traveled by the ball before it hits the ground?

Answer 1

The horizontal distance traveled by the ball before it hits the ground is 48.85 meters.

Step-by-step explanation:

It is given that,

Speed of golf ball, v = 25 m/s

Angle above horizontal or angle of projection, θ = 65°

We need to find the distance travelled by the ball before it hots the ground or in other words we need to find the range. It is given by R.

`R=(v^2\ sin2\theta)/(g)`

`R=((25\ m/s)^2\ sin2(65))/(9.8\ m/s^2)`

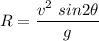
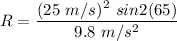
R = 48.85 m

So, the distance travelled by the ball before it hots the ground is 48.85 meters. Hence, this is the required solution.