Question

A ball is launched at an angle of 10 degrees from a 20 meter tall building with a speed of 4 m/s. How long is the ball in the air, how far from the launch point does it land, and what is the maximum height the ball reaches with respect to its starting height? a) -1.85 s,8.71 m, 1.54m b) 2.21 s, 8.71 m, 1.54m c) 6.44 s, 4.23 m, 0.02 m d) None of the above

Answer 1

d) None of the above

Step-by-step explanation:

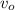`v_(o)` = inituial velocity of launch = 4 m/s

θ = angle of launch = 10 deg

Consider the motion along the vertical direction

`v_(oy)` = initial velocity along vertical direction = 4 Sin10 = 0.695

m/s

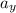`a_(y)` = acceleration along the vertical direction = - 9.8 m/s²

y = vertical displacement = - 20 m

t = time of travel

using the equation

`y=v_(oy) t+(0.5)a_(y) t^(2)`

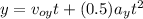
- 20 = (0.695) t + (0.5) (- 9.8) t²

t = 2.1 sec

consider the motion along the horizontal direction

x = horizontal displacement

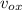`v_(ox)` = initial velocity along horizontal direction = 4 Cos10 = 3.94 m/s

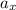`a_(x)` = acceleration along the horizontal direction = 0 m/s²

t = time of travel = 2.1 s

Using the kinematics equation

`x =v_(ox) t+(0.5)a_(x) t^(2)`

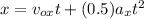
x = (3.94) (2.1) + (0.5) (0) (2.1)²

x = 8.3 m

Consider the motion along the vertical direction

`v_(oy)` = initial velocity along vertical direction = 4 Sin10 = 0.695

m/s

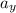`a_(y)` = acceleration along the vertical direction = - 9.8 m/s²

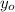`y_(o)` =initial vertical position at the time of launch = 20 m

`y` = vertical position at the maximum height = 20 m

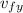`v_(fy)` = final velocity along vertical direction at highest point = 0 m/s

using the equation

`{v_(fy)}^(2)= {v_(oy)}^(2) + 2 a_(y)(y - y_(o))`

`0^(2)= 0.695^(2) + 2 (- 9.8)(y - 20)`

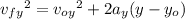
`y` = 20.02 m

h = height above the starting height

h =
`y` -
`y_(o)`

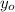
h = 20.02 - 20

h = 0.02 m