Question

A 280-g mass is mounted on a spring of constant k = 3.3 N/m. The damping constant for this damped system is b = 8.4 x 10^-3 kg/s. How many oscillations will the system undergo during the time the amplitude decays to 1/e of its original value?

Answer 1

The number of oscillation is 36.

Step-by-step explanation:

Given that

Mass = 280 g

Spring constant = 3.3 N/m

Damping constant
`b=8.4*10^(-3)\ Kg/s`

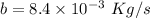
We need to check the system is under-damped, critical damped and over damped by comparing b with
`2m\omega_(0)`

`2m\omega_(0)=2m\sqrt{(k)/(m)}`

`2√(km)=2*\sqrt{3.3*280*10^(-3)}=1.92kg/s`

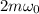
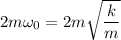
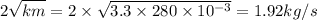
Here, b<<
`2m\omega_(0)`

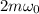
So, the motion is under-damped and will oscillate

`\omega=\sqrt{\omega_(0)^2-(b^2)/(4m^2)}`

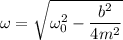
The number of oscillation before the amplitude decays to
`(1)/(e)` of its original value

`A exp((-b)/(2m)t)=A exp(-1)`

`(b)/(2m)t=1`

`t = (2m)/(b)`

`t=(2*280*10^(-3))/(8.4*10^(-3))`

`t=66.67\ s`

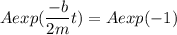
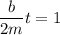
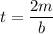
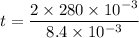
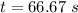
We need to calculate the time period of one oscillation

`T=(2\pi)/(\omega)`

`T=\frac{2*3.14}{\sqrt{\omega_(0)^2-(b^2)/(4m^2)}}`

`T=\frac{2*3.14}{\sqrt{(k)/(m)-(b^2)/(4m^2)}}`

`T=\frac{2*3.14}{\sqrt{(3.3)/(280*10^(-3))-((8.4*10^(-3))^2)/(4*(280*10^(-3))^2)}}`

`T=1.83\ sec`

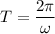
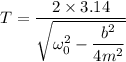
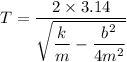
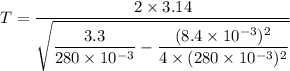
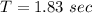
The number of oscillation is

`n=(t)/(T)`

`n=(66.67)/(1.83)`

`n=36`

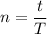
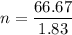
Hence, The number of oscillation is 36.