Answer:
The correct option is C.
Explanation:
If (x-c) is a factor of a polynomial f(x), then f(c)=0.
It is given that (x-1) is a factor of the polynomial. It means the value of the function at x=1 is 0.
In option A,
The given function is
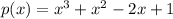
Substitute x=1 in the given function.
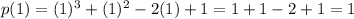
Since p(1)≠0, therefore option A is incorrect.
In option B,
The given function is

Substitute x=1 in the given function.
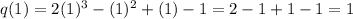
Since q(1)≠0, therefore option B is incorrect.
In option C,
The given function is
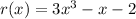
Substitute x=1 in the given function.

Since r(1)=0, therefore option C is correct.
In option D,
The given function is
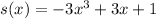
Substitute x=1 in the given function.
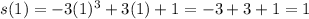
Since s(1)≠0, therefore option D is incorrect.