Question

An electron (mass m=9.11×10−31kg) is accelerated from the rest in the uniform field E⃗ (E=1.45×104N/C) between two thin parallel charged plates. The separation of the plates is 1.90 cm . The electron is accelerated from rest near the negative plate and passes through a tiny hole in the positive plate, with what speed does it leave the hole?

Answer 1

Step-by-step explanation:

It is given that,

Mass of an electron,
`m=9.11* 10^(-31)\ kg`

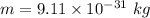
Electric field,
`E=1.45* 10^4\ N/C`

Separation between the plates, d = 1.9 cm = 0.019 m

The electron is accelerated from rest near the negative plate and passes through a tiny hole in the positive plate. We need to find the speed of the electron as it leave the hole.

The force due to accelerating electron is balanced by the electrostatic force i.e

qE = ma

`a=(qE)/(m)`

`a=(1.6* 10^(-19)\ C* 1.45* 10^4\ N/C)/(9.11* 10^(-31)\ kg)`

`a=2.54* 10^(15)\ m/s^2`

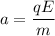
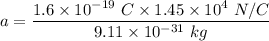
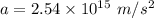
Let v is the speed as it leave the hole. It can be calculated using third equation of motion as :

`v^2-u^2=2ad`

`v=√(2ad)`

`v=\sqrt{2* 2.54* 10^(15)* 0.019\ m}`

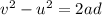
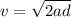
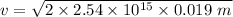
v = 9824459.27 m/s

or

`v=9.82* 10^6\ m/s`

So, the speed of the electron as it leave the hole is
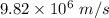`9.82* 10^6\ m/s`. Hence, this is the required solution.